XX საუკუნის მეცნიერების ისტორიაში ბევრია საინტერესო და საიდუმლოებით მოცული პრობლემა, რომელიც საბოლოოდ ბრწყინვალედ და საბოლოოდ იყო ამოხსნილი. მათ შორის საოცარი სიმარტივით და სილამაზით გამოირჩევა “კვადრატის კვადრირების” პრობლემა, რომელსაც ეს ნარკვევი ეძღვნება.
ამოცანა ასე ყალიბდება: ჩავთვალოთ რომ მოცემული გვაქვს კვადრატული ფორმის ზედაპირი, რომლის გვერდი მთელი რიცხვის ტოლია. ამოცანა მდგომარეოებს ამ ზედაპირის დაფარვაში კვადრატული ფორმის ფილებით, რომელთა გვერდის ზომა ასევე მთელი რიცხვია.
ეს ამოცანა რთული არაა, მაგრამ იგი საგრძნობლად რთულდება თუ დამატებით მოვითხოვთ, რომ ყველა იმ კვადრატული ფილის ზომა, რომელიც გამოიყენება ზედაპირის დასაფარად უნდა განსხვავებული იყოს ერთმანეთისგან. კვადრატის ასეთ კვადრირებას იდეალურს ეძახიან. თუ იდეალური კვადრირებისას გამოიყენება N ცალი სხვადასხვა ზომის კვადრატი, მაშინ N რიცხვს კვადრირების რიგი ჰქვია.
ეს ამოცანა პირველად დაისვა და შესწავლილი იყო 1936-1938 წლებში, კემბრიჯის უნივერსიტეტის ოთხი სტუდენტის – ბრუქსის, სმითის, სთოუნის და თათის – მიერ. ისინი ამ მათემატიკურ პრობლემას ფიზიკის პოზიციიდან მიუდგნენ: მათ კვადრატის კვადრირების ამოცანას შეუსაბამეს ანალოგური ელექტრული წრედი, რომელშიც თითოეული კვადრატი წარმოდგენილი იყო როგორც რეზისტორი (წინაღობა), რომელიც მეზობლებს ზედა და ქვედა კიდეებით ებმებოდა. შემდეგ ამ ანალოგურ წრედს მათ კირხჰოფის კანონები მიუყენეს და წრედის დეკომპოზიციის ტექნიკა გამოიყვანეს. ასეთნაირად მათ იპოვეს კვადრატის კვადრირების პირველი ვარიანტი, რომელიც 69 განსხვავებული კვადრატით ხერხდებოდა; შესაბამისად, მისი რიგი N = 69.
კვადრატის კვადრირების უფრო მცირე რიგის (ამავე დროს, პირველი გამოქვეყნებული ვარიანტი!) 1939 წელს აღმოაჩინა როლანდ სპრეგმა (Roland Spraggue). მისი კვადრატის გვერდის სიგრძე 4205-ის ტოლი იყო, ხოლო კვადრირების რიგი კი 55-ისა. პრობლემამ მსოფლიოს ყურადღება 1958 წელს მიიპყრო, როცა მათემატიკის განთქმულმა პოპულარიზატორმა მარტინ გარდნერმა ჟურნალ Scientific American-ის 1958 წლის ნოემბრის ნომერში, მათემატიკური თამაშების მის მიერ რედაქტირებულ გვერდზე გამოაქვეყნა თათის სტატია კვადრატის კვადრირების პრობლემის ადრეულ ისტორიაზე.
კვადრატის კვადრირების პრობლემა კიდევ უფრო რთულდება თუ მოვითხოვთ, რომ კვადრირებისას გამოყენებული კვადრატები არ ქმნიდენ კვადრატის შიგნით მცირე კვადრატს ან მართკუთხედს. ასეთ კვადრირებას მარტივს ეძახიან. ასეთი კვადრირება, თან დრამატულად შემცირებული რიგით, N = 24, აღმოაჩინა თეოფილუს უილკოკსმა (T.H. Willcocks). ეს იმდენად ეფექტური ვარიანტი იყო, რომ კარგა ხანს თვლიდნენ, რომ სწორედ ეს იყო კვადრატის იდეალური და მარტივი კვადრირება მინიმალური რიგით.
ამიტომ მათემატიკის სამყაროში მეხის გავარდნას ჰგავდა ჰოლანდიელი მათემატიკოსის, ინფორმატიკის სპეციალისტის, არი დეივესტეინის (A.J.W. Duijvestijn) საოცარი აღმოჩენა. მან რიცხვითი, კომპიუტერული მეთოდით 1978 წელს იპოვნა კვადრატის იდეალური და მარტივი კვადრირება, რომელიც ხერხდება 21 პატარა კვადრატით, ანუ კვადრირების რიგი N = 21!
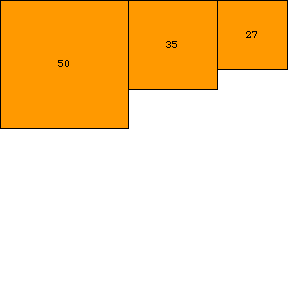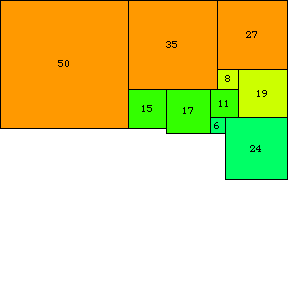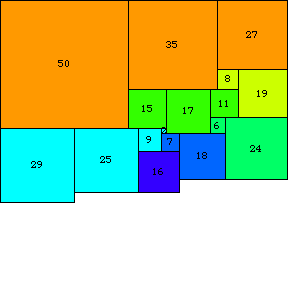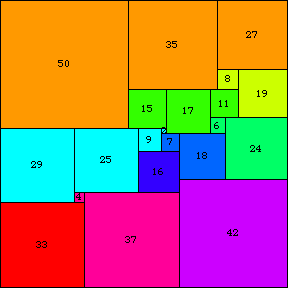
კიდევ უფრო მნიშვნელოვანი ისაა, რომ დეივესტეინმა, აქვე დაამტკიცა, რომ ეს კვადრირება მინიმალურია და ერთადერთია! კემბრიჯის მათემატიკურმა საზოგადოებამ (ე. წ. Trinity Mathematical Society), სადაც 40 წლით ადრე დაიბადა ეს ლეგენდარული პრობლემა, დეივესტეინის ეს გეომეტრიული შედევრი თავის ემბლემად აქცია (იხ. სურათი).

ჰოლანდიაში ეს აღმოჩენა დღემდე პოპულარულია და მათემატიკის მოყვარულთათვის სპეციალური, კვადრატული ფორმის კარადებიც კი დამზადდა, სადაც თაროები სწორედ დეივესტეინის კვადრირების წესით არიან აგებული (იხ. სურათი).

აქვე საინტერესოა აღინიშნოს, რომ ჯერ კიდევ კემბრიჯელმა ოთხეულმა დაამტკიცა, რომ კუბის კუბირება, ისევე როგორც უფრო მაღალი განზომილების, ე. წ. “ჰიპერკუბის” დაშლა ერთმანეთის არამსგავს კუბებად ან ჰიპერკუბებად შეუძლებელია! ამდენად ორგანზომილებიანი კვადრატი ერთადერთია, რომლისთვისაც ეს შესაძლებელია!
წყარო:
Mysterium Magnum, ივნისი 2018




