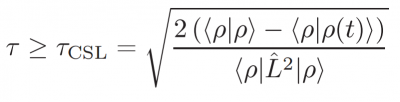
კვანტურ მექანიკაში იმპულსი და კოორდინატი აღიწერება ოპერატორებით რომლებიც არ კომუტირებენ (არ არიან გადასმადი), რასაც მივყავართ ჰაიზენბერგის განუზღვრელობის თანაფარდობაბმდე: Δx∙Δp ≥ ½|<[x,p]>| = ħ/2 (აქ სამკუთხა ფრჩხილები ნიშნავს სისტემის საშუალოს რაიმე მდგომარეობაში). კვანტურ მექანიკაში არაა განმარტებული დროის შესაბამისი ოპერატორო, თუმცა ხშირად განიხილავენ ასევე ე.წ. ჰაიზენბერგის მეოთხე განუზღვრელობის თანაფარდობას ენერგიისა და დროისათვის, ΔE∙Δt ≥ ħ/2, რომელსაც ზოგჯერ მოიხსენიებენ როგორც „სიჩქარის კვანტურ ზღვარს“ (Quantum Speed Limit, QSL). სიტყვა „სიჩქარე“ აქ ჩნდება ამ თანაფარდობიდან გამომდინარე სისტემის ევოლუციის დროზე შეზღუდვის გამო: Δt ≥ ħ/(2ΔE).

იაპონელმა თეორეტიკოსებმა Manaka Okuyama და Masayuki Ohzeki ჟურნალ Physical Review Letters ბოლო ნომერში გამოქვეყნებულ სტატიაში აჩვენეს, რომ „სიჩქარის კვანტურ ზღვარი“ განპირობებულია ფუნქციების სივრცის თვისებებით და არა ოპერატორების არაკომუტატურობით. მათ განიხილეს n-ნაწილაკის კლასიკური სიტემა, რომელიც აღიწერება დროზე დამოუკიდებელი ჰამილტონიანით. ასეთი სისტემის ევოლუცია განისაზღვრება განაწილების ფუნქციით ფაზურ სივრცეში ρ(t) და ლიუვილის ერმიტული ოპერატორით L, რომელიც კვანტურ-მექანიკური ჰამილტონიანის ანალოგიურია. განაწილეის ფუნქცია გაშალეს ლიუვილის ოპერატორის საკუთარი მნიშვნელობების მიხედვით და განიხილეს საბოლოო განაწილების ფუნქციის, ρ(t), პროექცია საწყის განაწილების ფუნქციაზე, ρ. შედეგად მიიღეს „სიჩქარის კვანტურ ზღვარის“ მსგავსი თანაფარდობა „სიჩქარის კლასიკური ზღვარი“ (CSL), რომელიც განპირობებულია ნაწილაკების დიდი რიცხვით და საწყისი და საბოლოო განაწილებების „გადაფარვით“.

მსგავსი თანაფარდობა მიღებული იქნა ასევე წყალში ნაწილაკების ბროუნის მოძრაობის შემთხვევისთვის და ავტორებმა დაასკვნე, რომ სიჩქარის ზღვარის არსებობა ზოგადი თვისებაა ყველა სისტემისთვის რომელთა ევოლუციაც აღიწერება ერმიტული ჰამილტონიანით და არ უკავშირდება ოპერატორების კომუტიციას.

წყარო:

https://journals.aps.org/prl/abstract/10.1103/PhysRevLett.120.070402