კვანტური ტელეპორტაცია

კვანტური გამოთვლების ერთეული არის ქუბიტი. ის შეიძლება წარმოვიდგინოთ, როგორც სისტემა ორი შესაძლო მდგომარეობით. სისტემის მდგომარეობა აღიწერება ორი კომპონენტისგან შემდგარი ვექტორით:

|φ› = a⋅|↑› + b⋅|↓› ,

a და b ნორმირებულია 1-ზე.

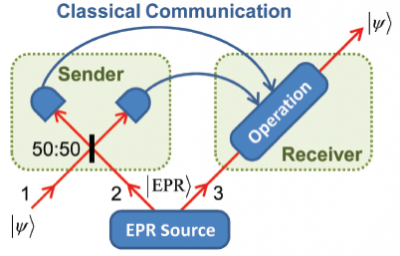
კვანტური ტელეპორტაციის მოვლენა არის კვანტური მდგომარეობის სივრცეში გადაცემა გადახლართული წყვილის მეშვეობით და ერთი კლასიკური კავშირის არხის გამოყენებით, რომლის დროსაც მდგომარეობა ირღვევა გაზომვისას გადაცემის წერტილში და აღდგება მიღების წერტილში. მისი იდეა დაფუძნებულია აინშტაინ-პოდოლსკი-როზენის პარადოქსზე (ეპრ), რაც გულისხმობს, რომ ორი გადახლართული ნაწილაკის მდგომარეობები დაკავშირებულია. მნიშვნელოვანია, რომ კვანტური ტელეპორტაციის დროს არ ხდება ენერგიის ან ნივთიერების გადაცემა.

კვანტური ტელეპორტაციის პრინციპის უკეთ გასაგებად ჩავატაროთ წარმოსახვითი ექსპერიმენტი. დავუშვათ, ალისას აქვს ნაწილაკი

|φ› = a⋅|↑› + b⋅|↓›

მდგომარეობაში, მაგრამ a და b მისთვის უცნობია. ალისას მიზანია, რომ მეორე დამკვირვებელ ბობს გაუჩნდეს ზუსტად იგივე მდგომარეობაში მყოფი ნაწილაკი. ამისთვის ალისას და ბობს გადაეცემათ გადახლართული წყვილის თითო ნაწილაკი, B და C (ეპრ-წყვილი). ასე ალისას აქვს ორი ნაწილაკი: A-გადასაცემი და B - გადახლართული წყვილის, ხოლო ბობს აქვს მარტო ერთი - C - გადახლართული წყვილის. ეპრ-პარადოქსის გათვალისწინებით, ალისა ახდენს თავისი ორი A და B ნაწილაკის სისტემის მდგომარეობის გაზომვას (ანუ იზომება ორი ნაწილაკის სისტემის პარამეტრები ისე, რომ ცალკე ნაწილაკის პარამეტრები არ იცვლება). ამ სისტემას ექნება 4 საბაზისო მდგომარეობა, რომლებსაც ავირჩევთ ასე:

1/√2(|↑ ↑› + |↓ ↓›),  1/√2(|↑ ↑› - |↓ ↓›),  1/√2(|↑ ↓› + |↓ ↑›),  1/√2(|↑ ↓› - |↓ ↑›).

რადგან გვაქვს გადახლართული ნაწილაკები, გამოვა რომ ბობის C ნაწილაკი იმყოფება შემდეგი ოთხი მდგომარეობიდან ერთ-ერთში:

a⋅|↑› ± b⋅|↓› ან b⋅|↑› ± a⋅|↓›.

სწორედ ამ დროს ხდება ინფორმაციის “კვანტური ნაწილის” გადაცემა. მაგრამ გადაცემული ინფორმაციის აღდგენა ჯერ შეუძლებელია: ბობმა იცის რომ A და C ნაწილაკების მდგომარეობები კავშირშია ერთმანეთთან, მაგრამ ამ კავშირის სახე უცნობია.  ამის დასადგენად საჭიროა, რომ ალისამ კლასიკური არხით გადაგზავნოს თავისი AB- გაზომვის შედეგი. ამგვარად გამოდის, რომ მიმღები ფლობს A და B ნაწილაკებზე ჩატარებული გაზომვის შედეგებს და B და C გადახლართული მდგომარეობის გაზომვას. ეს ინფორმაცია საკმარისია B-ს მდგომარეობის აღსადგენად და იქედან A-ს თავდაპირველი მდგომარეობის მისაღებად. სირთულეს წარმოადგენს ის, რომ ალისა ვერ გადასცემს თავის გაზომვის შედეგებს ბობს 100% სიზუსტით, რადგან გადაცემის არსი კლასიკურია. პრაქტირკულად, გამოდის, რომ ეპრ-წყვილის და 2 ბიტი კლასიკური ინფორმაციის წყალობით შესაძლოა ერთი ქუბიტი ინფორმაციის გადაცემა.

კვანტურ ტელეპორტაციაში პირველი თვალსაჩინო შედეგები დაიმზირა 2004 წელს, ხოლო 2015 წლის სექტემბერში აშშ-ს სტანდარტების და ტექნოლოგიების ნაციონალური ინსტიტუტის (NIST) მეცნიერებმა მოახერხეს ფოტონების ტელეპორტაცია ოპტიკური ბოჭკოში უკვე 100 კმ მანძილზე.

გამოყენებული ლიტერატურა:
1. http://thehackernews.com/
2. http://www.rec.vsu.ru/rus/ecourse/quantcomp/sem10.pdf
3. http://scorcher.ru/art/theory/quants/quants2.php